ROSETTA

Contents:
• Part I - Cuboids
• Part II - Spheres, Cylinders and Cone
• Part III - Pyramids and Prisms
• Part IV - Torus

So far we have only been working on the bi-dimensional plane but now we want to move on to something a bit more “volumetric”. Apart from the functions that create 2D entities Rosetta also provides functions for creating solid primitives.

For creating cuboids we have the choice of box , cuboid and right-cuboid . The function box will create a rectangular cuboid from the bottom-left corner and opposite top corner or from the bottom-left corner, length, width and height. Some of these parameters are optional so if the user only provides one point as argument the function will create a unitary cube positioned at the point (xyz 0 0 0). Likewise if the width is not provided the function will assume it has a unitary value. Below, in Figure 1 we can see an example of three cuboids created with different inputs:

(box)
(box (xyz 2 0 0) (xyz 4 2 3))
(box (xyz 5 0 0) 4 3 4)

FIGURE 1 | Three cuboids created with different parameters

In the function box the first point given is the bottom-left corner but suppose we want to create a cuboid with its base centred on a point. We could obviously calculate the necessary coordinates for that but to bypass that additional nuisance we can simply use the right-cuboid function.

(right-cuboid (xyz 0 0 0) 4 4 2)
(right-cuboid (xyz 0 0 2) 3 3 3)
(right-cuboid (xyz 0 0 5) 8)

FIGURE 2 | Three centred cuboids

Finally we have the function cuboid which creates any convex polyhedron bounded by its eight vertices. These vertices must be given in order, first the 4 base vertices and then the 4 top vertices.

(cuboid (xyz 0 0 0) (xyz 4 0 0) (xyz 4 2 0) (xyz 0 2 0)
        (xyz 0 0 4) (xyz 2 0 4) (xyz 2 2 4) (xyz 0 2 4))

(cuboid (xyz 5 0 2) (xyz 9 0 0) (xyz 9 2 0) (xyz 5 2 0)
        (xyz 5 1 4) (xyz 7 1 4) (xyz 7 2 4) (xyz 5 2 4))

(cuboid (xyz 10 0 0) (xyz 12 0 0) (xyz 12 2 0) (xyz 10 2 0)
        (xyz 9 1 4) (xyz 12 1 3) (xyz 12 2 4) (xyz 9 2 4))

FIGURE 3 | Three irregular cuboids

For creating sphere Rosetta provides the function sphere to which we must give the sphere’s centroid point and radius.

(sphere (xyz 0 0 0) 10)
(sphere (xyz 20 0 0) 6)
(sphere (xyz 34 0 0) 4)

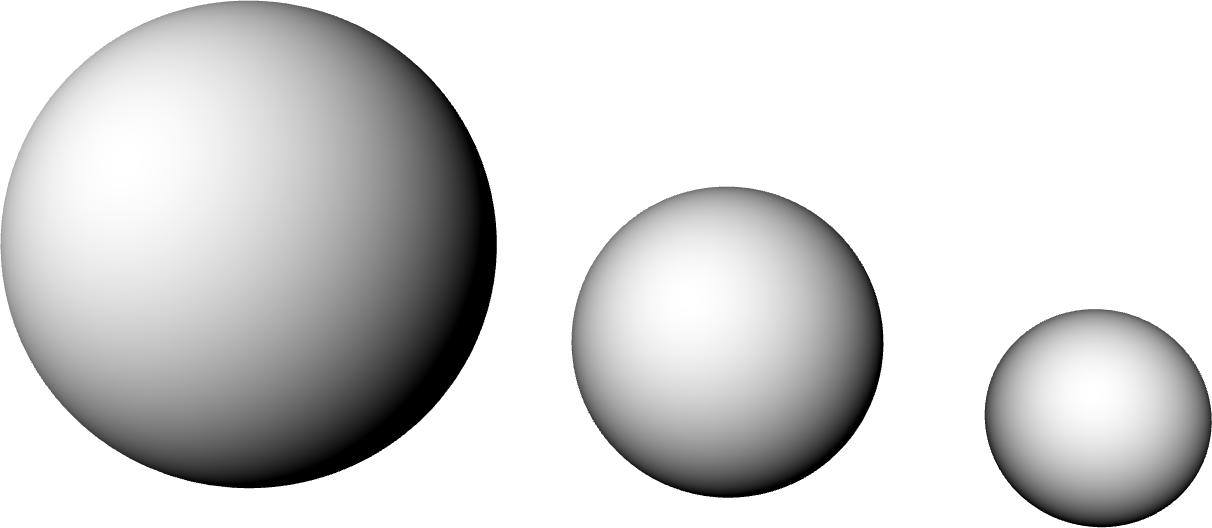
FIGURE 4 | Three spheres

We can also build cylinders using Rosetta’s cylinder function and here we can specify the base centre point, base radius and height, or alternatively, instead of the height, the location for the top centre point. If not aligned with the base centre point the cylinder will be tilted.

(cylinder (xyz 0 0 0) 2 1)

(cylinder (+xy (xyz 0 0 0) 8 0) 1 (xyz 0 0 8))
(cylinder (+xy (xyz 0 0 0) 0 8) 1 (xyz 0 0 8))
(cylinder (+xy (xyz 0 0 0) -8 0) 1 (xyz 0 0 8))
(cylinder (+xy (xyz 0 0 0) 0 -8) 1 (xyz 0 0 8))

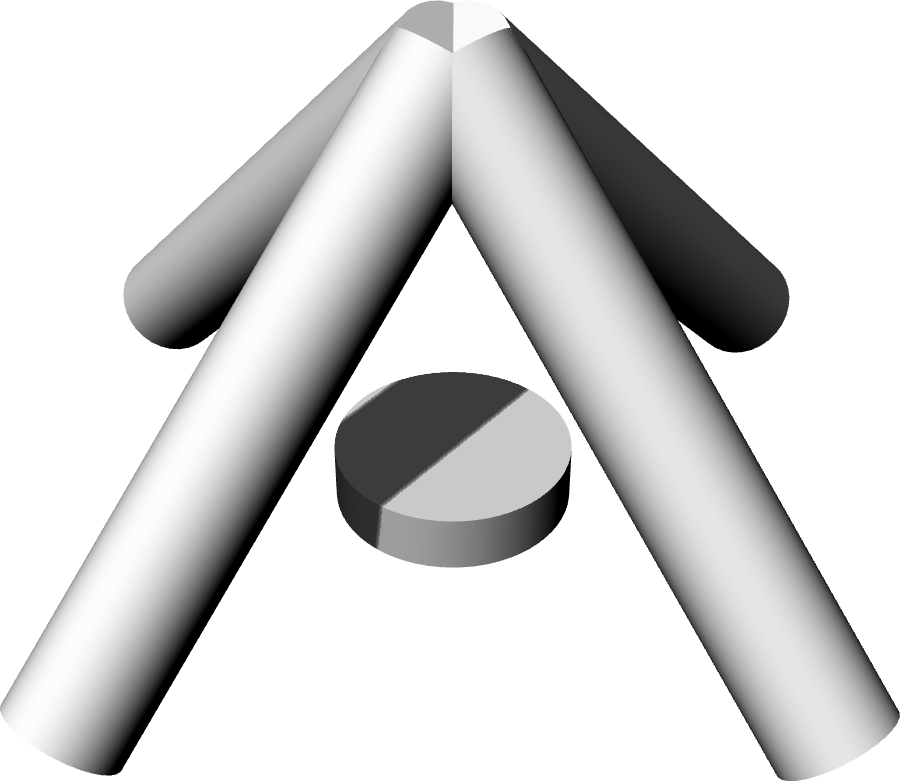
FIGURE 5 | A set of cylinders

If we want to create cones we can use the cone function and its variant cone-frustum . The first one will create a cone specified by the base centre point, base radius and height or alternatively by the base centre point, base radius and a second point for the cone’s tip. If this second point is not vertically aligned with the base point then the cone will be tilted.

(cone (xyz 0 0 0) 3 10)

(cone (xyz 8 0 0) 3 (xyz 14 0 10))
(cone (xyz 20 0 0) 3 (xyz 14 0 10))

FIGURE 6 | One straight cone and two other tilted

The second function will create a cone frustum, i.e., a sectioned cone, and it receives as parameters the base centre point, base radius, height and top radius or alternatively the base centre point, base radius, the top centre point and top radius.

(cone-frustum (xyz 0 0 0) 4 4 3)
(cone-frustum (xyz 0 0 4) 2 6 1)

(cone-frustum (xyz 8 0 0) 3 (xyz 10 0 4) 1)
(cone-frustum (xyz 10 0 4) 1 (xyz 12 0 8) 3)

FIGURE 7 | A set of cone frustums

The cone frustum is in fact a very interesting shape and by combining several we can create very intriguing shapes. For example, we want to define a function that creates crosses made up of 6 cone frustums, aligned in pairs with the orthogonal axes. We will consider for parameters the centroid point of this cross p, two radii for the base rb and top rt and finally a length c which will be the height of each cone. The function cross is thus defined:

(define (cross p rb rt c)
  (cone-frustum p rb (+x p c) rt)
  (cone-frustum p rb (+y p c) rt)
  (cone-frustum p rb (+z p c) rt)
  (cone-frustum p rb (+x p (- c)) rt)
  (cone-frustum p rb (+y p (- c)) rt)
  (cone-frustum p rb (+z p (- c)) rt))

We can now test this function with different values for the radii and length as shown in Figure 8:

FIGURE 8 | Examples of crosses made up of cone frustums

For creating pyramids Rosetta also provides the functions regular-pyramid for creating pyramids with a regular polygonal base, irregular-pyramid for creating pyramids with an irregular base and regular-pyramid-frustum for creating pyramid frustums with a regular base.

The regular-pyramid takes as parameters the number of sides, base centre point, base radius, base initial angle and height, or alternatively a second point, instead of the height, for the apex. Finally the regular-pyramid-frustum takes as parameters the number of sides, the base centre point, base radius, height and top radius or alternatively, instead of the height, the top radius.

(regular-pyramid 4 (xyz 0 0 0) 6 0 8)

(regular-pyramid-frustum 5 (xyz 20 0 0) 8 0 2 6)
(regular-pyramid-frustum 5 (xyz 20 0 3) 5 0 2 3)
(regular-pyramid 5 (xyz 20 0 6) 2.5 0 2)

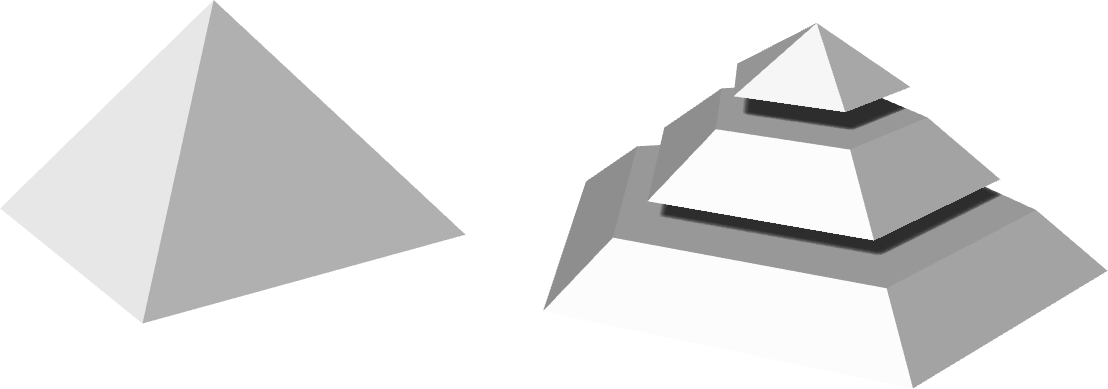
FIGURE 9 | Regular and pyramid frustums

The irregular-pyramid takes as parameters a list of points for defining the base, the apex location and an optional Boolean value to choose whether the final result is an open surface or a solid.

(irregular-pyramid (list (pol 5 0)
                         (pol 2 (/ 2pi 10))
                         (pol 5 (/ 2pi 5))
                         (pol 2 (+ (/ 2pi 10) (/ 2pi 5)))
                         (pol 5 (* (/ 2pi 5) 2))
                         (pol 2 (+ (/ 2pi 10) (* (/ 2pi 5) 2)))
                         (pol 5 (* (/ 2pi 5) 3))
                         (pol 2 (+ (/ 2pi 10) (* (/ 2pi 5) 3)))
                         (pol 5 (* (/ 2pi 5) 4))
                         (pol 2 (+ (/ 2pi 10) (* (/ 2pi 5) 4)))
                         (pol 5 (* (/ 2pi 5) 5))
                         (pol 2 (+ (/ 2pi 10) (* (/ 2pi 5) 5))))
                   (z 8))

FIGURE 10 | Regular and pyramid frustums

Next we have the functions for creating prisms. Here we also have the choice between a regular-prism and irregular-prism . The first receives as parameters the number of sides, base centre point, base radius, base initial angle and height, or alternatively the position of the top centre point. The later receives a list of points for defining the base and the prism’s height or alternatively the position of the top centre point.

(regular-prism 4 (xyz 8 0 0) 2 0 8)
(regular-prism 5 (xyz 16 0 0) 2 0 8)
(regular-prism 6 (xyz 24 0 0) 2 0 8)
(regular-prism 8 (xyz 32 0 0) 2 0 8)

(irregular-prism (list (xz 4 0) (xz 3 3)
                       (xz 0 6) (xz -3 3)
                       (xz -4 0))
                 (xyz 0 12 0))

FIGURE 11 | A set of prisms

And finally with have the function torus for creating torus specified by the centre point, the torus’ radius and ring section radius.

(torus (xyz 0 0 0) 10 2)
(torus (xyz 0 0 8) 8 2)
(torus (xyz 0 0 16) 6 2)

FIGURE 12 | Three tori

These solid primitives may seem very simple but they constitute some of the build block for modelling much more complex geometry. On way of doing so is by combining and manipulation them with each other. This technique of combing primitive solids, a process called also Constructive Solid Geometry, will be introduced in the next tutorial. By that we mean operations for performing unions, subtractions and intersections between geometric entities such as solids and surfaces. Click the link below when you are ready.