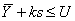
Uma classe de problemas em que a estatística t
não-central tem um papel importante é o cálculo de
curvas OC (curvas de característica operatória ou,
simplesmente, curvas características) para
inspecção por amostragem por variáveis.
Adapta-se, aqui, uma parte
--essencialmente, o seu ponto 4-a-- da monografia de Resnikoff e
Lieberman [1957].
Suponha-se que um artigo é classificado como
não-conforme (defeituoso) ou conforme (não-defeituoso) segundo se o valor
duma característica fica além (excede) ou fica
aquém duma especificação fixa,
U. A fracção não-conforme (def.), p,
num lote é definida como a fracção dos artigos que
caem acima de U. O problema geral da inspecção
por amostragem é a formulação dum procedimento que aceite
o lote se p for suficientemente pequeno. Em particular, a
inspecção por amostragem por variáveis pode ser usada
se a característica medida, Y, for uma variável
aleatória distribuída gaussianamente. (Note-se que
esta variável Y é distinta da variável
aleatória que dependa somente de o artigo ser defeituoso ou
não-defeituoso.) O procedimento de aceitação
para o caso em que a média, μ, e o desvio-padrão,
σ, são desconhecidos é aceitar o lote se for
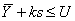
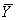 e s, média e desvio-padrão amostrais, calculados
duma amostra de dimensão n, serão dados por
e s, média e desvio-padrão amostrais, calculados
duma amostra de dimensão n, serão dados por
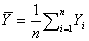
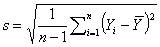
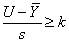
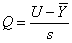
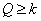
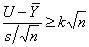
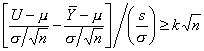
Ora a expressão do primeiro membro tem uma
distribuição t
não-central com
f = n - 1
graus de liberdade e parâmetro de descentramento
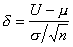 .
Convir-nos-á definir
.
Convir-nos-á definir
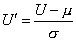 («normalização» de U). O
critério de aceitação virá
(«normalização» de U). O
critério de aceitação virá
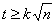
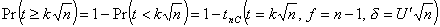
onde tnC é a
distribuição
t não-central acumulada. Caso se consulte a
própria tabela do integral de probabilidade de Resnikoff e
Lieberman [1957], isto é, tRL, haverá
que entrar com
x = 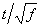 (em vez de t) e
p = 1 - Φ(U')
(em vez de δ), dando
(em vez de t) e
p = 1 - Φ(U')
(em vez de δ), dando
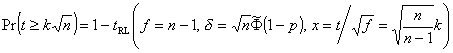
Como exemplo, calculam-se dez pontos da
curva OC(2)
—2.ª coluna da Tabela— para n = 10 e
k = 1,72. Os parâmetros para uso da
tabela
dos autores são f = n − 1 = 9,
p (o único que variará) e
x =
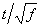 = 1,813. Recorde-se que
= 1,813. Recorde-se que
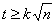 é equivalente a
é equivalente a
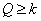 .
.
| Fracção def., p |
Prob. de aceitação, via tRL |
δ | Prob. de rejeição, via NAG, α |
Prob. de aceitação, via NAG, 1 − α | ||
| 0,0010 | 0,9961 | 9,77221 | 0,0038 | 0,9962 | ||
| 0,0025 | 0,9843 | 8,87672 | 0,0156 | 0,9844 | ||
| 0,0040 | 0,9692 | 8,38663 | 0,0306 | 0,9694 | ||
| 0,0100 | 0,8976 | 7,35654 | 0,1022 | 0,8978 | ||
| 0,0250 | 0,7177 | 6,19794 | 0,2823 | 0,7177 | ||
| 0,0400 | 0,5685 | 5,53616 | 0,4316 | 0,5684 | ||
| 0,0650 | 0,3851 | 4,78802 | 0,6151 | 0,3849 | ||
| 0,1000 | 0,2242 | 4,05262 | 0,7760 | 0,2240 | ||
| 0,1500 | 0,1038 | 3,27749 | 0,8964 | 0,1036 | ||
| 0,2500 | 0,0215 | 2,13293 | 0,9786 | 0,0214 |
Se recorrermos à função G01GBF da biblioteca NAG [1998], os argumentos são t = 1,72 √10 = 5,43912, f = n − 1 = 9 e δ = U'√n, obtendo-se α, probabilidade de rejeição, donde 1 − α, probabilidade de aceitação —última coluna da Tabela. Estes resultados concordam com os anteriores (provenientes de interpolações em tabelas) a menos, por vezes, de arredondamentos.
Compõe-se de: (1) introdução, (2) descrição das tabelas, (3) exemplos dos usos da função densidade de probabilidade da estatística t não-central, (4) exemplos do uso do integral de probabilidade e pontos percentuais da estatística t não-central, (4-a) inspecção por amostragem por variáveis para fracção defeituosa, com uma especificação dada, (4-b) inspecção por amostragem por variáveis para fracção defeituosa, com duas especificações dadas, (4-c) intervalos de confiança para proporções desde população gaussiana, (4-d) potência do teste t de Student, (4-e) o coeficiente de variação, (5) métodos computacionais, (6) tabela da função de densidade de probabilidade da estatística t não-central (145 págs.), (7) tabela do integral de probabilidade da estatística t não-central (204 pp), (8) tabela dos pontos percentuais da estatística t não-central.
(1) No caso de ser dado o
limite inferior de especificação, L (em vez
do superior, U), define-se
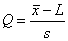 ,
o que permite manter o mesmo critério de
aceitação. (Note-se que não só se
substituiu U por L.) Assim, simplesmente, um
maior índice de qualidade corresponde sempre a uma melhor
qualidade.
,
o que permite manter o mesmo critério de
aceitação. (Note-se que não só se
substituiu U por L.) Assim, simplesmente, um
maior índice de qualidade corresponde sempre a uma melhor
qualidade.
(2) Este exemplo corresponde
—na norma ANSI/ASQC Z1.9-1980 (que substitui a MIL-STD-414),
Tabela
B-1—, ao plano de amostragem de letra de código F
(n = 10) e AQL de 1,00 %, no qual se
verifica um subjacente α = 10%. Neste plano,
os cálculos do exemplo apontam para um LTPD de (pouco superior a)
15% (β = 10%).
| Criado em: 2001-Nov — Actualizado em: 2005-Fev-12 |