Fibonacci Sequence: The Fast Doubling Method
The nth term of a Fibonacci sequence can be found through matrix operations. The general matrix form is given by:
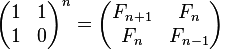
If one takes the determinant of both sides of the above equation, one can end up with the fast doubling formula:
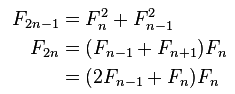
Just like in the matrix form method, the fast doubling algorithm runs in O( M(n) Log(n) ), where M(n) is the time for the multiplication of two numbers with n digits. The difference between this method and the closed-form matrix formula is the following: the doubling algorithm requires fewer redundant steps if one avoids to recompute an already computed Fibonacci number (recursion with memoization), making this algorithm one of the fastest methods to compute the Fibonacci sequence.
Several algorithms have been proposed to address the problem of multiplying very large integers. The most known algorithms are: the Karatsuba Multiplication, Toom-Cook and Schönhage–Strassen algorithm.
The algorithm that I chose to use was the Karatsuba fast multiplication algorithm. Later, I pretend to put an implementation of each of the above mentioned algorithms to compare performances.
My implementation of the fast doubling algorithm, to compute the nth element of the Fibonacci sequence, is the following: