Machine Learning

In my Master Thesis, I learned and worked a lot with machine learning. The ability of a computer learning by itself still amazes me and this is one of my favorite research topics. In this page, I will present the definition of machine learning as well as a detailed definition and application examples of several machine learning algorithms.

Table of Contents

• What is Machine Learning?
• Supervised Learning
• Support Vector Machines
• Neural Networks
• Decision Trees
• Random Forests
• Adaboost
• Unsupervised Learning
• Clustering: k-means
• Supervised Learning to Rank for Information Retrieval
• Based on Support Vector Machines
• SVMmap
• SVMrank
• Based on Neural Networks
• RankNet
• ListNet
• LambdaMart
• Based on Boosting Theory
• AdaRank
• RankBoost
• Based on Boosting Theory
• AdaRank
• RankBoost
• Regression Trees
• Random Forests
• Additive Groves
• Mart
• Others
• Coordinate Ascent

What is Machine Learning?

Arthur Samuel (1900 - 1990)

Arthur Samuel was an American researcher in the fields of computer games and artificial intelligence. He believed that computers could learn by experience. In 1959, he proposed a the world's first self-learning program: a Checkers-Playing game.

Since many professional checkers players had annotations of what would be examples of good plays and bad plays, Samuel used that data in order to adjust the criteria for his computer program. This was, the computer would only choose the plays that were consider good by expert players.

Samuel is also the inventor of several techniques in rote learning and generalization learning.

In his checkers program, Samuel used a search tree with the positions of the board that could be reachable from a current state. The learning function was a score that, based on the position of the board at specific given time, the function would measure the probability of each player winning. His program used as features things like the number of pieces on each side of the board, the number of kings and the pieces that were closed to be kings. The computer program used a minimax strategy. That is, the computer program would always choose a play assuming that the opponent would always choose the play that would give him more advantages (a higher score). Along his game, Arthur Samuel also proposed the first definition for machine learning:

Tom Mitchell (1951 - )

Supervised Learning To Rank for Information Retrieval

Information retrieval essentially deals with ranking problems. An adhoc retrieval system checks the documents of a collection and ranks them according to their degree of relevance to a user query expressing the information need. The major difficulty faced by an Information Retrieval (IR) system resides in the computation of these relevance estimates.

Learning to rank for information retrieval is a particular approach to the traditional information retrieval ranking problems. It automatically tunes parameters and builds ranking models through the usage of hand labelled training data (e.g., document collections containing relevance judgements for specific sets of queries), this way leveraging on data to combine different estimators of relevance in an optimal way. The learned raking model can then sort documents according to their degree of relevance to a given query. In the scope of information retrieval, learning to rank (L2R) methods can automatically help to sort documents according to the query topics.

The following figure provides an illustration of the general approach which is commonly used in most learning to rank methods. It consists in two separate steps, namely training and testing.

In this framework, q_i (i=1,...,n) corresponds to the set of n queries for the training step, x⁽ⁱ⁾= { x⁽ⁱ⁾_j }^m(i)_j=1, with m being the number of documents associated with query q_i, are the feature vectors associated to each query and yⁱ (i=1,...,n) are the corresponding set of relevance judgements. When applying a specific learning method to this training set, the system combines the different estimators of relevance in an optimal way, learning the corresponding ranking model. During the learning process, a loss function is applied to measure the inconsistencies between the hypothesis space h and the ground truth label y.

In the test step, the learned ranking model is applied to a new given query in order to sort documents according to their relevance to the information need. The ranked document set is then returned as a response to the query.

Learning to Rank algorithms can be classified into three major approaches: pointwise, pairwise and listwise approaches.

Pointwise Approaches

In pointwise approaches, since the relevance degrees can be regarded as numerical or ordinal scores, the learning to rank problem is seen as either a regression (the relevance degree is seen as a real number), classification problem (the ground truth label is regarded as a quantitative value).

The idea behind the pointwise approach is that given feature vectors of each single document of the training data for the input space, the relevance degree of each of those documents can be predicted with scoring functions, and throughout these scores one can sort all documents and produce the final ranked list. A loss function is applied in order to measure the individual inconsistencies between the scoring function and the ground truth labels. Many supervised machine learning algorithms for regression, classification or ordinal regression can be readily used for this purpose.

The advantage of the pointwise approach is that it directly supports the application of existing theories and algorithms on regression or classification. However, the information order between documents cannot be considered in the training step, because the algorithm receives single documents as input. Since evaluation measures in IR are based in two fundamental criteria, namely query-level and position-based data, this loss of document order information is a major problem, because the evaluation measures which take into account the position of the documents will not be directly optimized and, consequently, the pointwise approach may unconsciously overemphasize unimportant documents.

Pairwise Approaches

In pairwise approaches, since the relevance degree can be regarded as a binary value which tells which document ordering is better for a given pair of documents, learning to rank methods are seen as a classification problem. The general idea behind the pairwise approach is that given feature vectors of pairs of documents of the training data for the input space, the relevance degree of each of those documents can be predicted with scoring functions which try to minimize the average number of misclassified document pairs. The loss function used in the pairwise approach takes into consideration the relative order of each pair of documents.

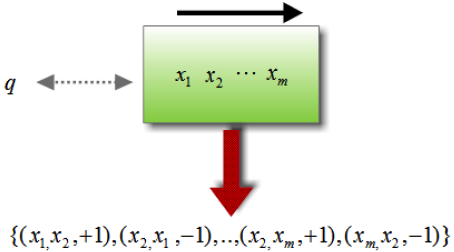
Notice that the classification problem that this approach addresses is not the same as the one addressed by the pointwise approach. In the pointwise approach, the learning method operates on every single document. On the other hand, in the pairwise approach, the learning method operates on every two documents under investigation.

The advantage of the pairwise approach is that it directly supports the application of existing theories and algorithms on classification. However, the loss function only takes into account the relative order of the pair of documents and therefore it is very difficult to derive the order of the documents in the final ranked list.

Listwise Approaches

In listwise approaches, the learning to rank problem takes into account an entire set of documents associated with a query as instances, and trains a ranking function through the minimization of a listwise loss function defined on the predicted list and the ground truth list.

The idea behind the listwise approach is that, given feature vectors of a list of documents of the training data for the input space, the relevance degree of each of those documents can be predicted with scoring functions which try to directly optimize the value of a particular information retrieval evaluation metric, averaged over all queries in the training data. The loss function used in the listwise approach takes into consideration the positions of the documents in the ranked list of all the documents associated with the same query. This is a difficult optimization problem, because most evaluation measures are not continuous functions with respect to the ranking model's parameters. Continuous approximations or bounds on evaluation measures have been successfully used in this task.

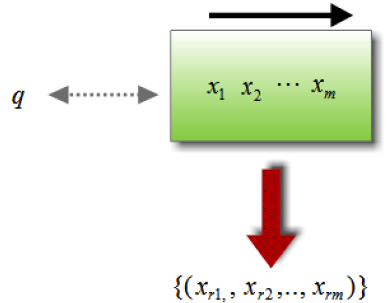
The major advantage that the listwise approach has over the pointwise and the pairwise approaches is that its loss function takes into account the positions of the documents in a ranked list of all documents associated with the query. Since evaluation measures in IR consider the document positions, this approach generally improves the performance.

Algorithms Based On Support Vector Machines

Support Vector Machines (SVMs) can also be defined as learning machines that construct an N-dimensional decision boundary surface that optimally separates data into positive examples and negative examples, by maximizing the margin of separation between these examples. One major advantage is the computational complexity of an SVM, which does not depend on the dimensionality of the input space.

SVMmap

The SVMmap listwise method, introduced by Yisong Yue and Thomas Finley, builds a ranking model through the formalism of structured Support Vector Machines, attempting to optimize the metric of Average Precision (AP).

The general idea of SVMmap is to minimize a loss function which measures the difference between the performance of a perfect ranking (i.e., when the Average Precision equals one) and the minimum performance of an incorrect ranking (i.e., when it is less than one).

The SVMmap algorithm receives as input the parameter $C$, which affects the trade-off between model complexity and the proportion of non-separable samples. If it is too large, we have a high penalty for non-separable points and we may store many support vectors and overfit. If it is too small, we may have underfitting.

Suppose x={x_j}_j=1^m is the set of all the documents associated with a training query q, and suppose that y_u,v⁽ⁱ⁾ represents the corresponding ground truth labels. Any incorrect label for x is represented as y^c. SVMmap solves the following quadratic optimization problem:

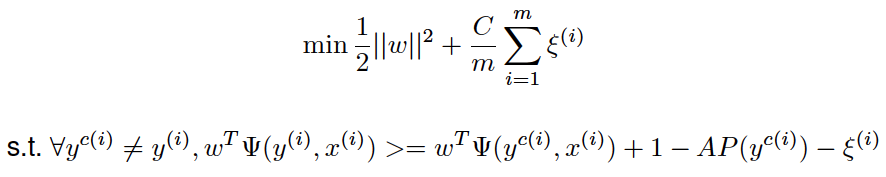
In Equation X, the margin term 1/2 ||w|| ² controls the complexity of the ranking model w. The method introduces slack variables, ξ_u,v ⁽ⁱ⁾, which measure the degree of misclassification of the datum x_i. Each time there is a wrong output $y$, SVMmap requires a constraint. In the constraints, Ψ(y,x) is called the joint feature map, whose definition is:

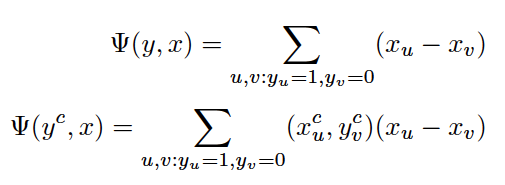
Since there are an exponential number of incorrect labels for ground truths, it is a big challenge to directly solve the optimization problem involving an exponential number of constraints for each query. In their work, the authors suggested the usage of the cutting plane method contained in the formalism of structured SVMs to efficiently tackle this issue by maintaining a working set with those constraints with the largest violation:

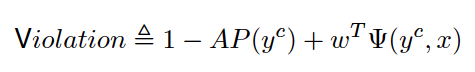
SVMrank

The basic idea of SVMrank is to attempt to minimize the number of misclassified document pairs. This is achieved by modifying the default support vector machine optimization problem, which considers a set of documents, by constraining the optimization problem to perform the minimization of each pair of documents. This optimization is performed by Equation X over a set of n training queries {q_i}_i=1ⁿ, their associated pairs of documents (x_u ⁽ⁱ⁾,x_v ⁽ⁱ⁾) and the corresponding relevance judgement y_u,v ⁽ⁱ⁾ over each pair of documents (i.e., pairwise preferences resulting from a conversion from the ordered relevance judgements over the query-document pairs):

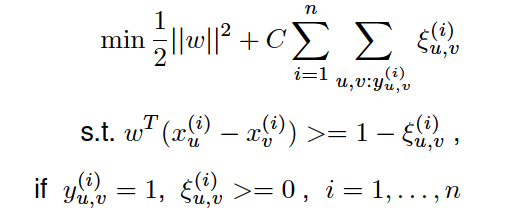
Differently from standard SVMs, the loss function in SVMrank is a hinge loss defined over document pairs. The margin term 1/2||w||² controls the complexity of the pairwise ranking model w. This method also introduces slack variables, ξ_u,v ⁽ⁱ⁾, which measure the degree of misclassification of the datum x_i.

The objective function is increased by a function which penalizes non-zero misclassifications, ξ_u,v ⁽ⁱ⁾, and the optimization becomes a trade off between a large margin, and a small error penalty.

Just like any SVM algorithm, SVMrank receives as input the parameter C which affects the trade-off between model complexity and the proportion of non-separable samples.

Algorithms Based On Neural Networks

RankNet