Project EULER Problem 1: Multiples of 3 and 5
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000.
My Solution
Looking at this problem for the first time, a person might think of a brute force approach to solve it: for all numbers from 1 to 999, just check which ones are multiples of 3 and 5 and sum them. For the limit 1000, a brute force approach would give an answer in a very short amount of time. However, if the limit is very large, then this approach is very inefficient.
Since I like programming challenges, I chose to implement an efficient method to solve this problem. My solution is based on the principle of inclusion/exclusion and in closed form summations. This way, we can reduce the total amount of operations to be performed.
A closed form summation is able to identify all multiples of a given number in the following way:
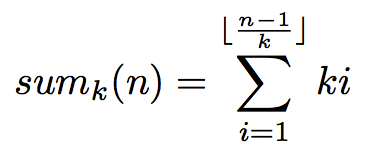
Using the principle of inclusion/exclusion, if we compute all multiples of 5 and all multiples of 3, we need to remove the intersection between these two sets, since their intersection will be added twice:
![]()