Catenary Brick Arches of Casa Milà
Original project: Antoni Gaudí
Programming Language: Julia
Algorithmic Design Tool: Khepri
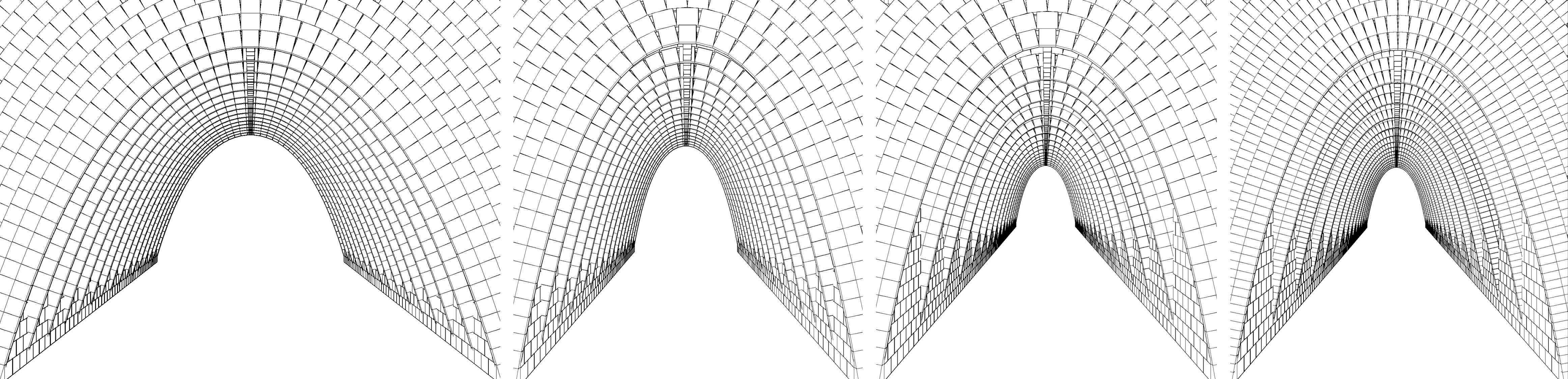
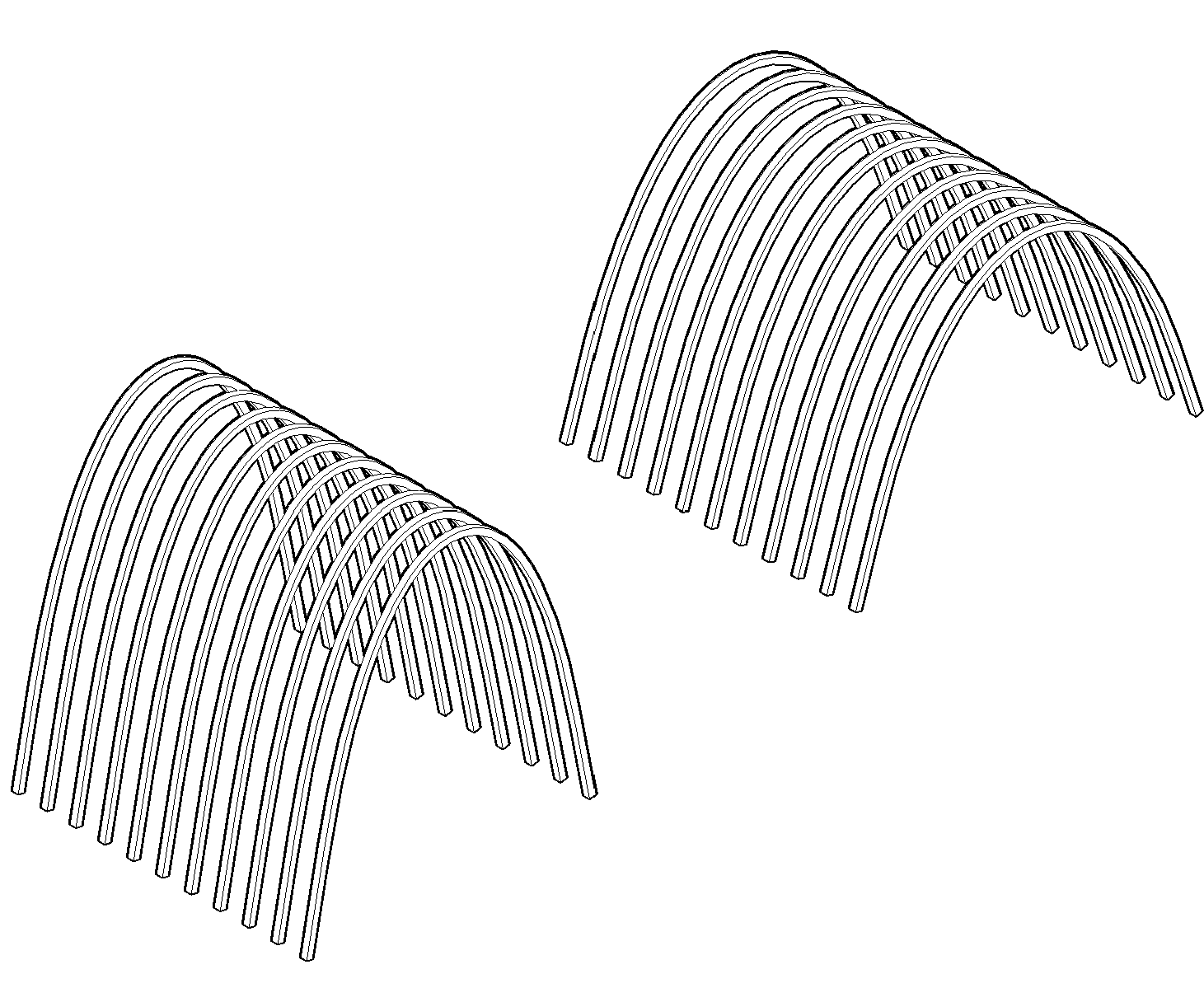
Mathematics has long been used in architecture, not only for simple tasks, such as calculating lengths, areas, volumes, and material quantities, etc., but also for more complex tasks, like exploring non-conventional shapes or creating geometric patterns. To evaluate the ability of the Algorithmic Design (AD) paradigm to represent mathematical concepts, we selected an example that applies a popular mathematical curve in architectural design: the catenary. Throughout history, architects have devised many ways of representing these curves, including drawings (descriptive geometry), physical models (e.g., Gaudi’s inverted chain model), and, more recently, digital models. For the catenary curve, we resort to Gaudí’s arches in Casa Milà in Barcelona, Spain.

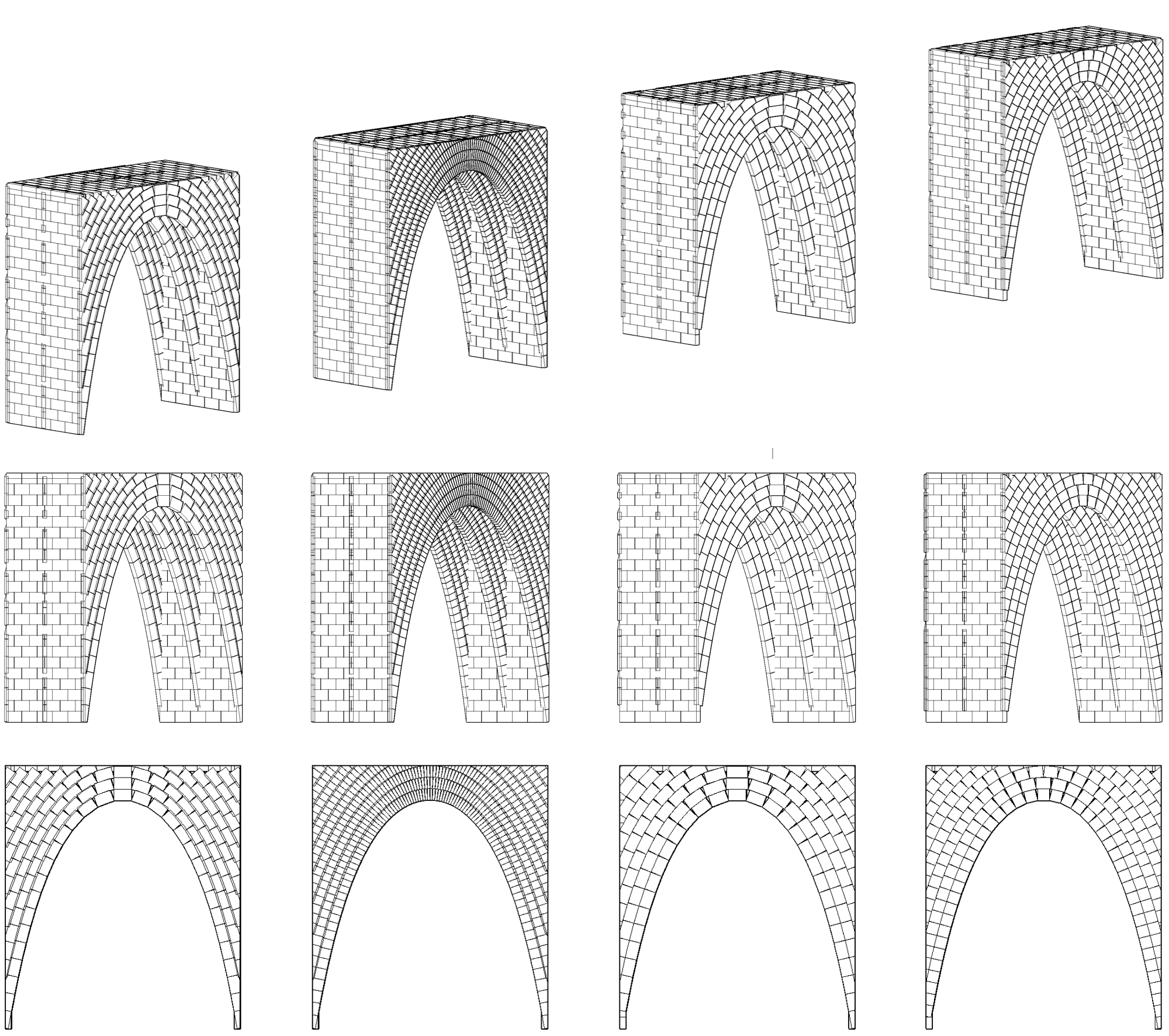
Representing the catenary brick arches in typical digital representation methods, such as Computer-Aided Drafting (CAD) and Building Information Modeling (BIM), requires manually calculating the spatial locations defining the intended curve and then materializing the arches along those locations. In the BIM paradigm, in particular, the task is more complicated because, in addition to the manual calculation of the curve’s locations, there are no standard construction elements available that suit the task. Therefore, modelling the catenary shape arches requires either the creation of objects with no semantics or a series of elaborate steps to create new BIM families with the desired shape.
In contrast, representing the same example in the AD paradigm requires parametrically describing the mathematical curve and using it to automatically guide the creation of the bricks along the arches. The catenary curve can be represented by the function catenary(x) = α×cosh(x/α), where cosh represents the hyperbolic cosine function and α its aperture factor. When testing different design variations, this parametric description automatically calculates new locations and generates the bricks accordingly. This not only makes the whole process faster and more flexible, but also less error-prone and tedious.