Fully-Compressed Suffix Trees

Luís M. S. Russo, Gonzalo Navarro, Arlindo L. Oliveira

Abstract:

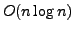
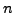
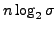
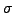
Suffix trees are by far the most important data structure in stringology, with myriads of applications in fields like bioinformatics and information retrieval. Classical representations of suffix trees require $O(n \log n)$ bits of space, for a string of size $n$. This is considerably more than the $n \log_2\sigma$ bits needed for the string itself, where $\sigma$ is the alphabet size. The size of suffix trees has been a barrier to their wider adoption in practice. 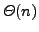Recent compressed suffix tree representations require just the space of the compressed string plus $\Theta(n)$ extra bits. 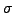This is already spectacular, but still unsatisfactory when $\sigma$ is small as in DNA sequences.

In this paper we introduce the first compressed suffix tree representation that breaks this linear-space barrier. Our representation requires sublinear extra space and supports a large set of navigational operations in logarithmic time. An essential ingredient of our representation is the lowest common ancestor (LCA) query. We reveal important connections between LCA queries and suffix tree navigation.