A Compressed Self-Index using a Ziv-Lempel Dictionary

Luís M. S. Russo, Arlindo L. Oliveira

Abstract:

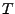
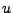
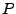
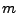
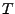
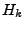
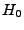
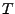
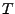
A compressed full-text self-index for a text $T$ , of size $u$ , is a data structure used to search for patterns $P$ , of size $m$ , in $T$ , that requires reduced space, i.e. space that depends on the empirical entropy ($H_k$ or $H_0$ ) of $T$ , and is, furthermore, able to reproduce any substring of $T$ . 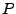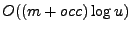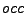In this paper we present a new compressed self-index able to locate the occurrences of $P$ in $O((m+occ)\log u)$ time, where $occ$ is the number of occurrences. 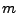The fundamental improvement over previous LZ78 based indexes is the reduction of the search time dependency on $m$ from $O(m^2)$ to $O(m)$ . 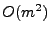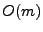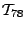To achieve this result we point out the main obstacle to linear time algorithms based on LZ78 data compression and expose and explore the nature of a recurrent structure in LZ-indexes, the $\mathcal{T}_{78}$ suffix tree. We show that our method is very competitive in practice by comparing it against other state of the art compressed indexes.