Cubic equation
Jan J. Tuma, 1989AD, "Handbook of Numerical Calculations in Engineering", McGraw-Hill, New York, 6.03, "Algebraic and transcendental equations", p 122

(a) General case

cub26
with real coefficients and cub27, reduces to

cub28

where

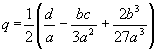cub29 cub30

and the roots of the original equation are

cub31 cub32 cub33

in which y1, y2, y3 are the roots of the reduced equations computed by (c) and (d) below.

(b) Classification of roots

With cub34 and a, b, c, d real, then if

D > 0 There is 1 real root and 2 conjugate complex roots
D = 0 There are 3 real roots, of which at least 2 are equal
D < 0 There are 3 real unequal roots

(c) First root of the original equation is always real and occurs in one of the following forms:

Case Conditions x1
1 d = 0 0
2 q = 0 cub35
3 D > 0 p > 0 cub36
4 p = 0 cub37
5 p < 0 cub38
6 D = 0   cub39
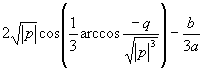7 D < 0   cub40

(d) Second and third roots of the original equation are the roots of the quadratic equation

cub41 cub44

with

cub42 cub43

(e) Relations of roots (as confirmation)

cub45 cub46 cub47
 v
Last update: 18-Jan-2001