Simulates, via Monte Carlo
(limited time), the distances from the source point on the horizontal axis
to N destination random points in a unit circle,
in order to find the distribution of the distance, d.
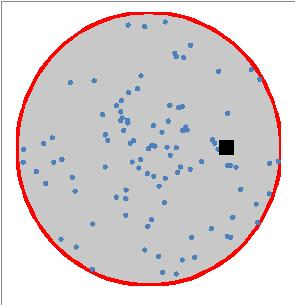
In the Figure, is shown a circle with the source point
(black, at x = 0.6) and N = 100 random points
(in the figure, from random polar coordinates).
The random destination points were computed through
ρ.(cosθ, sinθ)
from the following [Anon., 2014] algorithm:
ρ = rand1 + rand2;
if (ρ > 1) ρ = 2 − ρ;
θ = 2 π rand0 .
The particular case of x0 = 0 leads to
f(d) = 2d [Dartmouth, 2014],
as is here suggested from experimenting.
Plots the density function (pdf), f(d), and
the probability function (cdf), F(d),
for the distance, d, and computes its mean and standard-deviation. |
 |



