Integrates, via the Monte Carlo technique,
a function of 2 variables, i.e., calculates a volume,
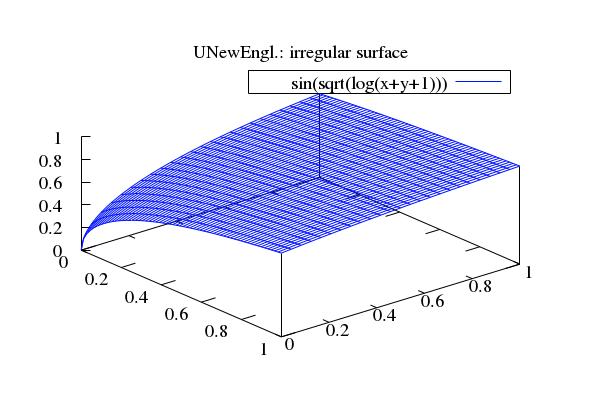
from [AMTH142], p 7: an elliptical cylinder topped by an
"irregular" surface (Fig.), given by
z = sin(√[ln(x + y + 1)]).
The (vertical) elliptic cylinder
([(x − a) ⁄ a]² +
[(y − b) ⁄ b]² = 1,
not shown)
has section tangent to both x- and y-axes,
with center at (a, b). The original problem has
a = b = 1⁄2.
The Monte Carlo integration technique is simple
and advantageous for dimensions of 2 or more. (The classical
numerical methods such as Simpson's rule are better
for one-dimensional integration.)
A plot is drawn showing the (random) progress
of the simulation towards its final value.
Other suggested data: (0.5, 0.5), giving
V ≅ 0.568. |
 |



