|
Minimum 2-leg distance
"within an angle"
Calculates a minimum 2-leg distance within the sides of an angle. |
|
|
| γ |
(driven to 0 ≤ γ < 90°) |
Angle (see figure): degrees or
{*} (π⁄2)radians. |
| x2 |
(x1 = 1;
x2 ≥ x1) |
Abscissa of B (end point). |
| Graph type |
(D* ≡
Dmin) |
D (distance) vs. x; or D* vs. γ;
or D* vs. x2. • |
| xuser |
|
Sample user value. • |
| xright |
|
Graph goes from 0 to xright
(auto. iff 0). • |
| Show values |
|
Shows the coordinates of the graph. • |
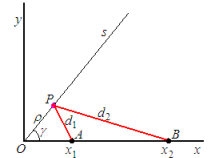
Calculates the minimum distance
"within (the sides of) an angle" (see figure),
D = d1 + d2, to go from
A, with (fixed) x1 = 1, to
B, with x2, both on the x axis
(first side of the angle),
passing by P, to be determined, on the half-line s
(second side), given the angle γ and
x2. [γ := |MOD(γ, 90|°).]
Point P, with radial coordinate ρ, is found
by differentiation (D' = 0), the solution
being x:
x−1 = ½
(x1−1 +
x2−1) sec²γ.
Counterintuitively, as γ → 0,
x tends to the harmonic, not the arithmetic mean. Also,
as x2 → ∞,
x = 2 x1 cos² γ.
A graph is made vs. t for either:
(a) D vs. t = x (x ≥ 0); or
(b) Dmin vs. (varying) t = γ
(0 to 90°); or
(c) Dmin vs. t = x,
x ≥ x1.
(This plate arose as a template.) |
 |
|
| References: |
Plate: AngDist2 |
• Weisstein, Eric W., "Minimum", from
MathWorld —a Wolfram Web Resource (2008-01-01).
• Mathews, John H.: Method:
(Isaac) Newton
-(Joseph) Raphson (California State Univ. Fullerton).
• 1822-01-02: Clausius, Rudolf J. E., birthday.
|