
O algoritmo do caixeiro-viajante |
Expresso 10-Março-2001 |
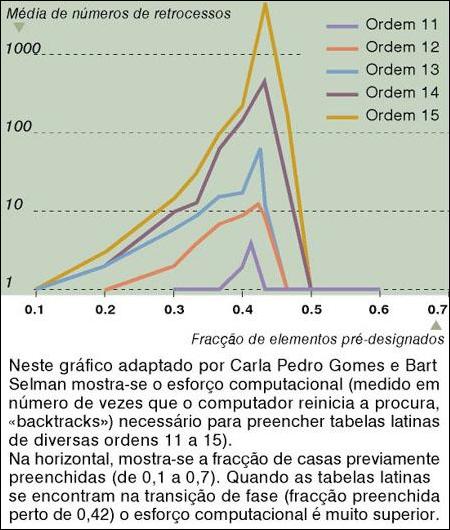
| Em computação, há problemas fáceis e problemas difíceis. Há também os muito difíceis. Conhecer a fronteira entre o possível e o quase impossível pode evitar muitos esforços inúteis. Texto de Nuno Crato | |
Quando os computadores começaram a poder resolver sistematicamente
alguns problemas numéricos, os matemáticos, lógicos e cientistas da
computação procuraram medir o seu grau de dificuldade.
Para isso, começaram a aplicar métodos sistemáticos de resolução
—os chamados algoritmos — e a medir o tempo
ou o esforço computacional necessário para alcançar uma resposta.
Uma das primeiras surpresas estaria reservada a Richard Karp que,
em fins dos anos 50, verificou que alguns problemas aparentemente simples
se podem tornar rapidamente intratáveis à medida que o número de
variáveis aumenta.
Karp, então no centro de investigação da IBM, procurava encontrar
circuitos óptimos, com um número mínimo de componentes,
e reparou que isso não era difícil de conseguir quando os percursos
desse circuito eram em número limitado. No entanto, à medida que o número
de circuitos possíveis aumentava, Karp reparou que os computadores eram
impotentes para encontrar uma solução em tempo útil.


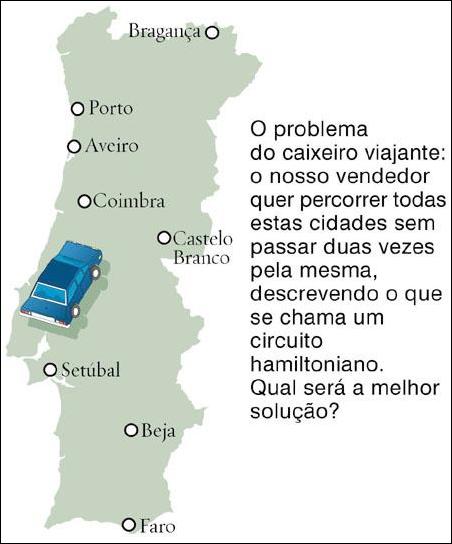
Um famoso problema deste tipo é o do caixeiro-viajante.
Se um caixeiro tiver de visitar várias cidades, é natural que procure
o caminho mais curto e que evite passar duas vezes pela mesma localidade.
Com meia dúzia de cidades a visitar, o nosso caixeiro não terá problemas
em descobrir uma solução óptima. Puxando pela cabeça e olhando para o mapa
das estradas, acabará por encontrar o percurso total mais curto.
O tempo que passou a pensar, poupar-lhe-á muitos quilómetros de estrada.
Há algoritmos que indicam um método de pesquisa e comparação das soluções
e que, programados em computador, permitem obter uma solução óptima em
fracções de segundo.
O que é bastante mais estranho é que o esforço computacional da verificação
de existência de uma solução aumenta desmesuradamente com o número de cidades
a visitar. Problemas deste tipo são chamados NP,
por contraste com os problemas de tipo P, ou polinomiais,
em que a dificuldade cresce moderadamente com o número de parâmetros.
Nos problemas de tipo P, se duplicarmos o número de parâmetros,
podemos esperar que o tempo de execução do algoritmo duplique,
ou quadruplique, sendo essencialmente proporcional a alguma
potência do número de parâmetros. Nos problemas de tipo NP,
a complexidade computacional é assustadora. Ao princípio, multiplicando
por dois o número de parâmetros, o problema pode demorar apenas
o dobro do tempo a ser resolvido. Se multiplicarmos de novo por dois
esse número de parâmetros, pode bem acontecer que a dificuldade seja
multiplicada por dez. E, se tentarmos de novo duplicar a dimensão do problema,
pode ser que o seu tempo de resolução seja multiplicado por 1000!
Os problemas de tipo NP parecem crescer de dificuldade
de uma maneira exponencial.
O nosso caixeiro-viajante defronta-se com uma tarefa deste tipo.
De tal forma que, se tiver de viajar por toda a Europa, não há
computador no mundo que lhe permita encontrar o melhor percurso a tempo
de fazer negócio. O melhor é fazer-se à à estrada, mesmo que
isso lhe custe um pouco mais de gasolina do que a solução óptima.
A distinção entre os problemas relativamente fáceis e os muito difíceis
é uma questão que ocupa há muito os especialistas. Recentemente,
os físicos Scott Kirkpatrick e Bart Selman, que têm trabalhado em problemas
de complexidade computacional, encararam esta matéria com uma nova abordagem.
Tirando partida da sua formação como físicos, trouxeram às ciências da
computação o conceito de transição de fase, originado na termodinâmica
e aplicado em várias áreas da física.
Quando a água congela, ou quando ferve, os físicos dizem que ela transitou
de fase. Os estados sólido, líquido ou gasoso da água são relativamente
fáceis de caracterizar, e o seu comportamento dentro de cada um
destes estados é relativamente bem conhecido. No entanto, o que
se passa nos momentos de congelação ou nos momentos de
evaporação é bastante mais difícil de compreender. Kirkpatrick e Selman
verificaram que o que se passa com muitos problemas computacionais
é muito semelhante: os problemas são simples de resolver quando se encontram
num «estado» ou num outro, mas tornam-se extraordinariamente
difíceis na transição de fase.
Um bom exemplo pode ser dado com o preenchimento de uma tabela
latina. Trata-se de um quadrado ou matriz, com igual número de linhas
e de colunas, como se exemplifica na figura. Tomemos como exemplo uma
matriz de quatro linhas e quatro colunas. Cada linha tem de ser
preenchida com quatro símbolos diferentes, de entre quatro
possíveis, suponhamos os símbolos 1, 2, 3 e 4. E em cada
linha não pode haver repetições. O mesmo se passa
com as colunas. Cada coluna tem de esgotar os quatro símbolos,
que não se podem repetir dentro da mesma coluna. Se a matriz
estiver vazia, é muito fácil preenchê-la. Pode, por
exemplo, escrever-se na primeira linha 1,2,3,4. Na segunda, 2,3,4,1; na
terceira, 3,4,1,2; na quarta 4,1,2,3.
Se a matriz estiver quase toda preenchida, é também
fácil completar a tabela latina ou, pelo contrário, chegar
à conclusão que essa tarefa é inglória, por
estarem as casas preenchidas de tal forma que não é
possível encontrar uma solução. Os problemas
aparecem quando a matriz está meio preenchida. Nessa altura, as
restrições podem ser tais que encontrar uma
solução ou verificar que não há
solução possível pode ser uma tarefa trabalhosa,
especialmente se a matriz tiver uma dimensão apreciável.
Bart Selman e Carla Pedro Gomes, uma especialista portuguesa em
ciências da computação, estudaram a fundo o problema
de preenchimento de tabelas latinas, que é um protótipo de
muitos problemas práticos de computação. Os dois
especialistas, que são actualmente investigadores na Universidade
de Cornell, chegaram à conclusão que a transição de fase se observa
quando as matrizes estão preenchidas a cerca de 40%.
Perceber a complexidade computacional deste tipo de problemas é
muito importante, pois as tabelas latinas são um modelo para muitos
problemas práticos de afectação de recursos, desde
o planeamento de voos e escalonamento do pessoal de bordo à
realização de experiências estatísticas.
Suponhamos, por exemplo, que temos quatro pneus de marcas
diferentes que queremos testar. Podemos colocá-los na mesma
viatura e verificar o seu desgaste ao fim de mil quilómetros de
estrada. Mas pode acontecer que os pneus da frente se gastem mais
depressa que os traseiros. E pode também acontecer que os pneus
do lado esquerdo sejam mais propensos ao desgaste, por suportarem um
peso ligeiramente maior. é necessário então mudar a
posição dos pneus e voltar a conduzir outros mil
quilómetros. Depois disso, será necessário
experimentar uma nova posição, e ainda uma outra,
até que cada pneu tenha estado uma e uma só vez em cada
roda. Só depois disso a observação do desgaste de
cada tipo de pneu pode ser conclusiva. Se cada linha da nossa matriz
representar uma posição dos quatro pneus
e cada coluna representar uma roda, a nossa experiência preenche
uma tabela latina.
Com uma matriz de quatro por quatro, os problemas são simples de
resolver. Mas, mesmo num exemplo tão simples como o dos quatro pneus
num carro, percebe-se que a matriz é mais fácil de preencher quando
está vazia do que quando está parcialmente preenchida. Se
iniciarmos a experiência a partir do zero, ou seja, sem termos testado
ainda os pneus, é fácil determinar uma sequência de posições. Mas,
tendo já rodado com os pneus numa e noutra posição, encontrar a
solução da tabela latina, ou seja, estabelecer as posições
seguintes dos pneus, pode obrigar-nos a pensar alguns segundos.
Os problemas complicam-se enormemente quando as matrizes
aumentam de dimensão. Experimente o leitor preencher parcialmente uma
tabela latina de dez por dez. E tente depois encontrar uma
solução. Verá que não é fácil. E os problemas práticos têm, muitas
vezes, matrizes de dimensão muito maior.
Saber de antemão quais são os problemas computacionais fáceis,
quais são os difíceis e quais são os muito difíceis, não nos ajuda
a encontrar uma solução. Mas, ao menos, dá-nos uma
ideia do que se pode esperar. Dessa forma pode-se avaliar o tempo que o
computador nos levará a resolver um problema ou, nos piores
casos, se será realista procurar uma solução.
 |
 |
http://web.ist.utl.pt/~mcasquilho/acad/or/Exp-caixv.php Created: 2006-03-01 — Last modified: 2009-03-18 |