98.07.21

Dimensionamento e Optimização de Equipamento

 

Nome:                                                                                                                          Nº:                  

 

Problema 1

 

Para determinar o teor de cobre numa solução, por absorção atómica, calibrou-se o aparelho com soluções padrão, obtendo-se as seguintes leituras em função da concentração:

 

C (ppm)	1,0	1,5	2,0	3,0
y	3,0	3,8	5,4	8,4

 

a) Se quiser estimar a leitura do aparelho para a concentração de 2,5 ppm com um erro inferior ou igual a 10 %, quantos padrões deveria preparar para a recta de calibração (y = f (C))?

 

b)  Deduza a expressão do somatório dos quadrados dos desvios (S) para a recta de calibração, obrigando-a a passar pelo ponto (0,02;0).

Calcule os valores dos parâmetros da equação.

 

 

 

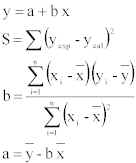
Problema 2

 

Uma fábrica tem de decidir se compra ou aluga um determinado equipamento, que lhe vai permitir possuir uma maior competitividade face às empresas concorrentes.

O equipamento novo custa 5.000 contos, tem uma vida útil de quatro anos e pode ser amortizado linearmente neste período.

O equipamento vai permitir à fábrica um acréscimo nas receitas de 2.000 contos/ano.

Os custos de manutenção são de 600 contos/ano.

O mesmo equipamento alugado custa 1.600 contos/ano.

A taxa de imposto é de 52 %.

A taxa de actualização é de 10 %.

 

Diga, justificando qual das opções escolheria.

 

 

 

Problema 3

 

A tabela seguinte mostra a planificação factorial, na qual se mostram duas variáveis quantitativas, temperatura e concentração de reagente e a variável qualitativa, o catalisador, que influenciam o rendimento de uma reacção.

 

Experiência	Temperatura (ºC)	Concentração (%)	Catalisador	Rendimento (g)
1 2 3 4 5 6 7 8	160 180 160 180 160 180 160 180	20 20 40 40 20 20 40 40	A A A A B B B B	60 72 54 68 52 83 45 80

 

 

Indique as variáveis por ordem de significância e quais os níveis óptimos para maximizar o rendimento.