©
The beta distribution
    Presents some calculations of parameters of the beta distribution.
 
a, b Parameters a and b of the distribution (0 < a, b ≤ 10^6).
μ, σ, CoeffVar Mean, standard deviation, and coefficient of variation of the distribution. •
Source a, b   μ, σ  μ, CoeffVar (Choose source data couple.)
x1, x2 Interval (from x1 to x2) for which probability will be calculated.
tol Tolerance for calculation of probability.
  For the beta distribution, its parameters (a, b), moments (mean, standard deviation), and coefficient of variation are calculated.  Once a certain source data couple is chosen, the other data are ignored.
  The formulas are, with ρ the coefficient of variation:
Source: Formulas
a, b 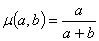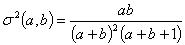μ σ
μ, σ a b
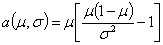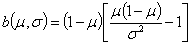μ, ρ a b
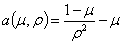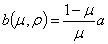  The parameters must obey certain conditions.  While any combination of a and b (positive) is valid, it must be 0 < μ < 1, of course, and σ < σmax = √[μ(1−μ)].  (Too large a σ leads to negative a, b.)
References:
•World of Mathematics
 
 
Valid HTML 4.01! IST http://web.ist.utl.pt/~ist11038/compute/qc/F.betaparams.php
Created: 2003-09-05 — Last modified: 2007-09-16