Draws the graph of an “inverse Gaussian”
distribution, not to be confounded with the inverse of the Gaussian,
or "normal", integral. The curves for the pdf and,
optionally, the cdf are shown.
The value corresponding to a given cumulative distribution is
calculated (via Newton-Raphson). (If it is p = 1, 0 is
assumed.) Too small σ may obstruct the calculation.
The formulas are:
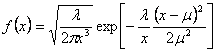 with with
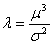 or
or
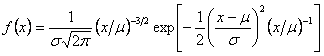
-L.gif) or or
-S.gif) |
|
• Aminzadeh, M. S., 1996, "Inverse-Gaussian
acceptance sampling plans by variables", Communications in Statistics
— Theory and Methods, 25(5), pp 923–935.
• Das, T. K.,
A. Gosavi, K. M. Kanchibhatta,
2002, "Optimal design of plans for acceptance sampling by variables with
inverse Gaussian distribution", Communications in Statistics
— Simulation, 31(3), pp 463–488. |



