Description

MDC-ELLIPSOIDs is a MATLAB^® code to calculate the minimum distance between two ellipsoidal surfaces in a non-conformal contact situation. The implemented methodology is specifically designed for rigid contact detection where the surfaces are in a convex-convex interaction and do not deform or alter there local geometric properties whenever there is contact. Therefore, in rigid contact, surfaces may share a common geometric locus, i.e., surfaces may overlap.

Minimum distance calculation is performed by numerically solving a system on non-linear equations with the Newton-Raphson method with analytical Jacobians. The system of non-linear equations corresponds to a set of necessary, although not sufficient, geometric constraints whose solution consists of the pair of points that have a common normal direction. To restrict the solution space to a unique pair of points, different types of constraints are considered: collinear constraint (vector cross-product); orthogonal constraint (vector inner-product); and locus constraint (point belongs to surface). To guarantee unicity, an additional non-equality condition, that evaluates the distances of all the candidate solutions, is considered. All constraints have a well-defined analytical expression that relate the geometric entities envolved in the common normal concept, i.e., the normal, tangent, binormal and distance vectors which are deducible given only the implicit surface functional.

Contact detection is performed by simply evaluating the sign of the minimum distance between the surfaces. The three types of contact detection statuses are: (i) no contact (surfaces appart ⇒ minimum distance greater than zero); (ii) external contact (contact at a single point ⇒ minimum distance equal to zero); and (iii) contact (surfaces overlap ⇒ minimum distance lesser than zero).

Householder transformation proved to be useful to deduce the tangential and binormal vectors given the analytical expression of the normal vector which, by vector calculus, is derived as the gradient of the implicit function. The Householder transformation is used to provide a base of three orthogonal vectors, in which one of them is collinear to the surface normal.

Proximity queries were also implemented to test for coarse (with the traditional bounding spheres) and narrow (with the separate condition) contact detection. Note that the proximity queries do not calculate the minimum distance between ellipsoids.

Applications The MDC-ELLIPSOIDs code was originally developed to perform computational simulations for contact analysis of multibody systems. However, the proposed methodology has important applications in many other areas of applied science such as, molecule simulation in computational physics, modeling discontinuous mechanical systems (discrete element method) in geomechanics, humanoid design in biomechanics, virtual reality simulation and computer animation.

Main characteristics of the MDC-ELLIPSOIDs methodology: surfaces are represented implicitly; mathematical framework relies on intuitive algebraic and differential geometry and vector calculus; numerical framework relies on the Newton-Raphson method; Jacobian matrix is calculated analytically (contributes for the geometric accuracy of the result and to the computational efficiency, since no matrix estimate is required for each iteration.); Jacobian matrix is non-singular in the neighborhood of the solution; highly efficient code (quadratic convergence); highly accurate results; convergence behaviour depends on the initial approximation (initial approximation must be close to the solution to guarantee convergence); is not a polyhedral-based contact detection method; does not rely on complex non-linear optimization formulations and methodologies; conformal (concave-convex) rigid contact can be detected if the relative curvatures between the surfaces allows a single solution; introduces the Householder transformation to calculate the tangent and binormal vectors given the normal vector expression; introduces a parametric representation for surface visualization that is generic for any member of the quadric family (i.e., ellipsoids, paraboloids, hyperboloids); easily extendable to other surfaces that satisfy all the following criteria: . are strictly convex or convex; . interact in a convex-convex (non-conformal) fashion; . possess an implicit representation; . are C2 continous and are twice differentiable (i.e., smooth surfaces).

Multibody Dynamics with Contact Forces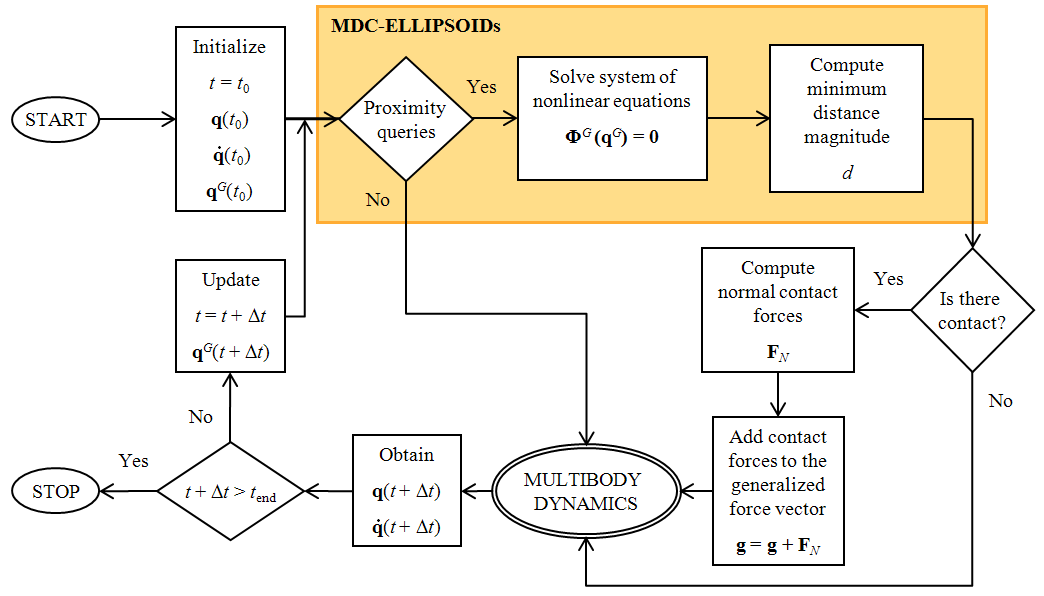 Flowchart of the MDC-ELLIPSOIDs integrated with a Multibody Dynamics module.

References

• A detailed description of the mathematical and computacional aspects is presented in the authors paper submitted to the Multibody System Dynamics journal:
  D.S. Lopes, M.T. Silva, J.A. Ambrósio, and P. Flores, A mathematical framework for contact detection between quadric and superquadric surfaces, Multibody System Dynamics, 24(3): 255 — 280, 2010. (DOI: 10.1007/s11044-010-9220-0)


• More information regarding the separate condition can be found in:
  Y.-K. Choi, J.-W. Chang, W. Wang, M.-S. Kim, G. Elber, Continuous Collision Detection for Ellipsoids, IEEE Transactions on Visualization and Computer Graphics, 15(2):311-325, 2009.


• The paper were the Householder transformation first appeared:
  A.S. Householder, Unitary Triangularization of a Nonsymmetric Matrix, Journal of the ACM, 4(5):339–342, 1958.

Download

Download MDC-ELLIPSOIDs, unpack it to a prefered directory and run it in the MATLAB^® environment. The directory is added automatically to your MATLAB path. Type 'mdcdemo' on the command line window for a quick demonstration. For more details see the corresponding documentation. Download MDC-ELLIPSOIDs [284 KB zip file]!

MDC-ELLIPSOIDs is licenced under a Creative Commons Attribution-NonCommercial-ShareAlike 2.0 Generic License.
See the License and Copyright notice for more information on authors acknowledgment and commercial use.

• D.S. Lopes, M.T. Silva, J.A. Ambrósio, and P. Flores, A mathematical framework for contact detection between quadric and superquadric surfaces, Multibody System Dynamics, 24(3): 255 — 280, 2010. (DOI: 10.1007/s11044-010-9220-0)
  
• MDC-ELLIPSOIDs Users and Developers Manual (PDF)
• Function Reference (HTML)

Gallery

Still images

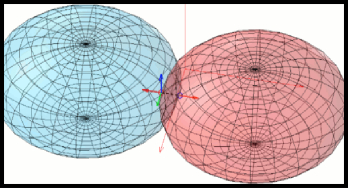
Videos

© 2010 Daniel Simões Lopes