Lesson22

Uma árvore AVL é uma árvore binária de pesquisa em que, para cada nó interno, a altura (height) de ambos os filhos difere, no máximo, em 1.

Análise

Seja $N(h)$ o número mínimo de nós numa árvore AVL com altura $h$. É fácil de verificar que $N(1) = 1$ e que $N(2) = 2$. Por definição, temos que $N(h) \geq N(h-1)$ e, considerando que a altura dos dois filhos de um nó difere no máximo em 1, obtemos $$ N(h) \geq N(h − 1) + N(h − 2) + 1 \geq 2 N(h − 2) + 1 > 2 N(h − 2)$$ Por indução, temos então que $N(h) > 2^i N(h - 2i)$ e, em particular, para $i = h/2 - 1$, obtemos $N(h) > 2^{h/2}$. Logo, aplicando o logaritmo, obtemos $h < 2\log N(h)$ e, portanto, a altura de uma árvore AVL é $O(\log N)$.

Inserção em árvores AVL

Antes demais é preciso notar que a inserção de novos elementos pode desequilibrar a árvore. Por exemplo, no caso do exemplo acima, ao inserirmos a chave $1$, obtemos a seguinte árvore desequilibrada:

Portanto pode ser necessário corrigir após a inserção de um novo elemento. A inserção em árvores AVL funciona da seguinte forma:

1. inserir o novo elemento, numa folha, como numa BST normal;
2. percorrer o caminho desde a nova folha até à raiz e
   1. para cada nó encontrado, verificar se as alturas dos dois filhos (esquerdo e direito) não diferem em mais do que 1
   2. e, se diferirem, equilibrar a sub-árvore com raiz nesse nó, efectuando uma rotação simples ou uma rotação dupla;
3. após equilibrar a sub-árvore com raiz num determinado nó $x$, não será necessário equilibrar as sub-árvores com raiz nos antecessores de $x$;
4. terminar após uma operação de equilíbrio, ou quando atingirmos a raiz.

No exemplo anterior basta fazer uma rotação à direita no nó com a chave 12, ou seja,

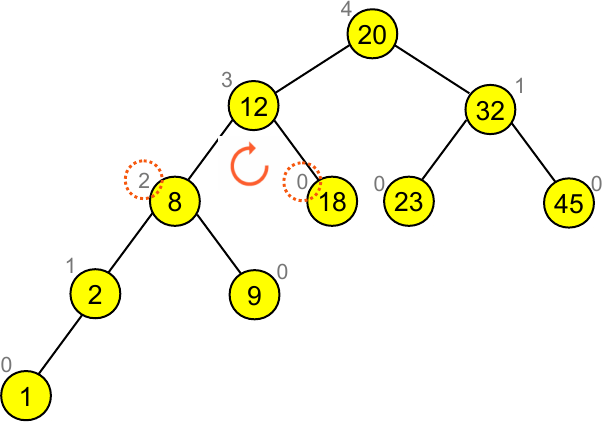
para obter a árvore equilibrada

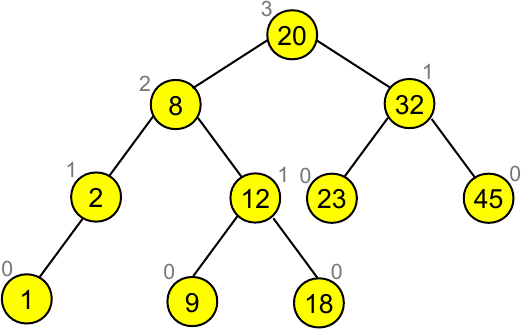
Rotações em árvores AVL

Pode ser necessário fazer uma rotação simples, à esquerda

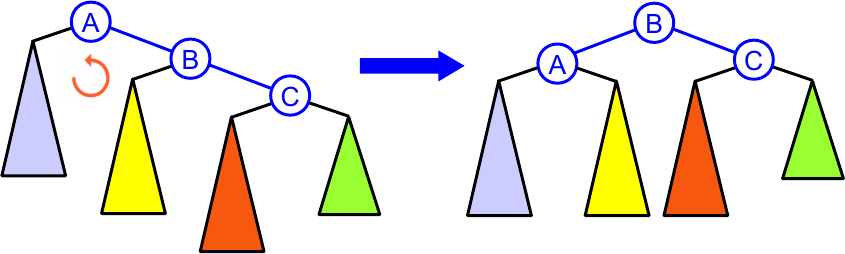
ou à direita

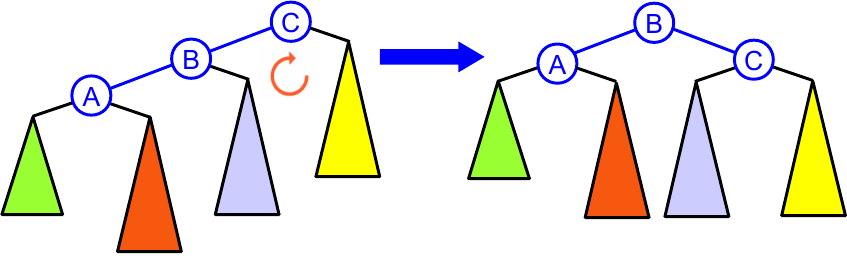
Ou pode ser necessário fazer uma rotação dupla, direita-esquerda

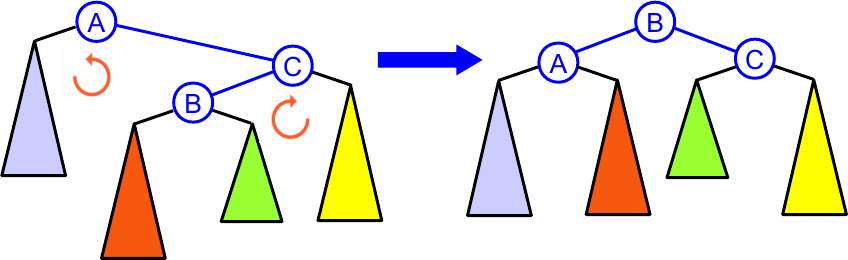
ou esquerda-direita

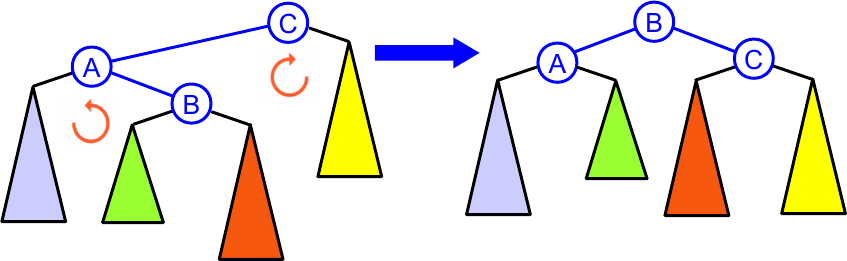
Casos de aplicação (na inserção):

1. Se o novo nó é inserido na sub-árvore da esquerda, da sub-árvore da esquerda do elemento desequilibrado, basta-nos aplicar uma rotação simples para a direita aplicada a esse elemento.
2. Se o novo nó é inserido na sub-árvore da direita, da sub-árvore da direita do elemento desequilibrado, basta-nos aplicar uma rotação simples para a esquerda aplicada a esse elemento.
3. Se o novo nó é inserido na sub-árvore da direita, da sub-árvore da esquerda do elemento desequilibrado, fazemos uma rotação dupla esquerda-direita.
4. Se o novo nó é inserido na sub-árvore da esquerda, da sub-árvore da direita do elemento desequilibrado, fazemos uma rotação dupla direita-esquerda.

Remoção em árvores AVL

Tal como na inserção, a remoção de um elemento pode desequilibrar a árvore. Por exemplo, se removermos a chave $45$ na árvore

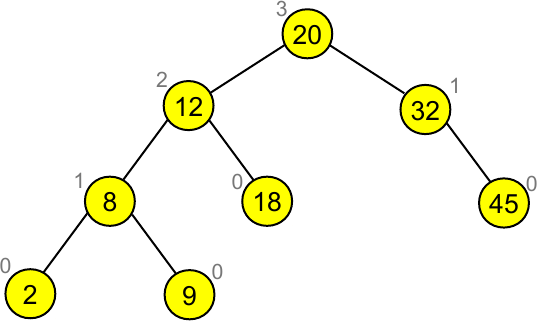
obtemos a seguinte árvore desequilibrada

Por forma a garantir as propriedades de uma árvore AVL, a remoção funciona da seguinte forma:

1. remover um nó como numa BST normal;
2. percorrer o caminho desde o nó removido até à raiz e
   1. para cada nó encontrado, verificar se as alturas dos dois filhos (esquerdo e direito) não diferem em mais do que 1
   2. e, se diferirem, equilibrar a sub-árvore com raiz nesse nó, efectuando uma rotação simples ou uma rotação dupla.
3. após equilibrar a sub-árvore com raiz num determinado nó $x$, poderá ser necessário equilibrar as sub-árvores com raízes nos antecessores de $x$;
4. terminar apenas quando atingirmos a raiz.

Complexidade das operações sobre árvores AVL

Antes demais é importante notar que cada operação para equilibrar, quer seja através de rotação simples ou dupla, decorre em tempo $O(1)$. Notar também que a pesquisa é realizada como numa árvore BST normal e que, em particular, não altera a árvore, decorrendo em tempo $O(\log N)$ dado que como vimos acima a altura de uma árvore AVL é também $O(\log N)$.

A inserção em árvores AVL decorre em $O(\log N)$ tempo dado que procurar a posição para inserir é $O(\log N)$ e manter a árvore equilibrada é $O(\log N)$ (subir na árvore e equilibrar uma única vez).

A remoção em árvores AVL decorre em $O(\log N)$ tempo dado que procurar o elemento a remover é $O(\log N)$ e manter a árvore equilibrada é $O(\log N)$ (subir na árvore e equilibrar no máximo $O(\log N)$ vezes).

Exercício

Construa uma árvore AVL inserindo os seguintes elementos (por esta ordem):

63, 9, 19, 27, 18, 108, 99 e 81

Desenhe a árvore equilibrada resultante, e escreva o resultado de uma travessia pré-ordem sobre essa árvore.

Implementação

Ficheiro ST.h:

#ifndef _ST_
#define _ST_

#include <stdlib.h>
#include <stdio.h>

#include "Item.h"

typedef struct STnode* link;

void STinit(link*);
int STcount(link);
Item STsearch(link, Key);
void STinsert(link*, Item);
void STdelete(link*, Key);
void STsort(link, void (*visit)(Item));
void STfree(link*);
#endif

Ficheiro ST.c com apenas as funções modificadas ou novas em relação à implementação das BST:

#include "ST.h”

struct STnode {
  Item item;
  link l, r;
  int height; /* altura do no */
};

link NEW(Item item, link l, link r)
{
  link x = (link) malloc(sizeof(struct STnode));
  x->item = item;
  x->l = l;
  x->r = r;
  x->height=1;
  return x;
}

int height(link h){
  if (h == NULL) return 0;
  return h->height;
}

link rotL(link h) 
{
  int height_left, height_right;
  link x = h->r;
  h->r = x->l;
  x->l = h;

  height_left = height(h->l);
  height_right = height(h->r);
  h->height = height_left > height_right ? height_left + 1 : height_right + 1;

  height_left = height(h->l);
  height_right = height(x->r);
  x->height = height_left > height_right ? height_left + 1 : height_right + 1;

  return x;
}

link rotR(link h) 
{
  int height_left, height_right;
  link x = h->l;
  h->l = x->r;
  x->r = h;

  height_left = height(h->l);
  height_right = height(h->r);
  h->height = height_left > height_right ? height_left + 1 : height_right + 1;

  height_left = height(x->l);
  height_right = height(h->r);
  x->height = height_left > height_right ? height_left + 1 : height_right + 1;

  return x; 
}

link rotLR(link h) /*rotação dupla esquerda direita*/
{
  if (h==NULL) return h;
  h->l=rotL(h->l);
  return rotR(h); 
}

link rotRL(link h) /*rotação dupla direita esquerda*/
{
  if (h==NULL) return h;
  h->r=rotR(h->r); 
  return rotL(h); 
}

/* balance factor, i.e., diferenca entre as alturas */
int balance(link h) { 
  if (h == NULL) return 0; 
  return height(h->l)-height(h->r); 
} 

link AVLbalance(link h) {    
  int balanceFactor, height_left, height_right;

  if (h==NULL) return h;

  balanceFactor = balance(h); 

  if (balanceFactor > 1) { 
    if (balance(h->l) > 0) h = rotR(h); 
    else                   h = rotLR(h);  
  } 
  else if (balanceFactor < -1) { 
    if (balance(h->r) < 0) h = rotL(h); 
    else                   h = rotRL(h); 
  } else {
    height_left = height(h->l);
    height_right = height(h->r);
    h->height = height_left > height_right ?  height_left + 1 : height_right + 1;
  }

  return h; 
} 

link insertR(link h, Item item) 
{
  if (h == NULL) 
    return NEW(item, NULL, NULL);
  if (less(key(item), key(h->item)))
    h->l = insertR(h->l, item);
  else 
    h->r = insertR(h->r, item);

  h = AVLbalance(h);

  return h;
}

link deleteR(link h, Key k) {
  Item x;

  if (h==NULL) return h;    
  else if (less(k, key(h->item))) h->l=deleteR(h->l,k);
  else if (less(key(h->item), k)) h->r=deleteR(h->r,k) ;
  else{
    if (h->l != NULL && h->r != NULL){
      link aux = max(h->l);

      x = h->item;
      h->item = aux->item;
      aux->item=x;

      h->l = deleteR(h->l, key(aux->item));
    } else {
      link aux=h;
      if (h->l == NULL && h->r == NULL) h = NULL;
      else if (h->l == NULL) h = h->r;
      else h = h->l;
      deleteItem(aux->item); 
      free(aux);
    }
  } 
  h = AVLbalance(h);

  return h;
}