Ainda que em situações ideais uma árvore binária possa garantir tempo $O(\log n)$ para as operações usuais sobre mapas associativos, existem casos em que tal não acontece com tempos de acesso $O(n)$ no pior caso. Estes casos surgem em geral quando as árvores binárias não estão balanceadas ou equilibradas, com o pior caso a ocorrer quando estão degeneradas. Para percebermos o que é uma árvore binária degenerada basta pensar no que acontece se inserirmos elementos com chaves ordenadas por ordem crescente (ou decrescente). Qual é o tempo de inserção e de pesquisa nesse caso?
NOTA: No que se segue, dada uma árvore binária, pressupõe-se que:
- a profundidade (depth) de um nó é o número de arcos entre esse nó e a raiz e, portanto, a raiz tem profundidade 0;
- a altura (height) de um nó é o número nós no caminho mais longo desse nó até uma folha, em que uma folha tem altura 0.
Por forma a garantir o tempo $O(\log n)$ queremos por norma manter as árvores equilibradas, em particular com recurso a árvores auto-equilibradas, em que se procura minimizar a altura das mesmas enquanto sujeitas a operações de inserção e remoção.
Uma árvore diz-se perfeitamente equilibrada se, para qualquer nó da mesma, a diferença entre o número de nós das sub-árvores é no máximo 1. Neste caso a altura da árvore é mínima em relação ao número de nós da mesma.
No entanto, manter uma árvore perfeitamente equilibrada implica um custo elevado nas operações, pelo que vamos discutir algumas estratégias que procuram minimizar a altura e garantir o tempo $O(\log n)$, sem no entanto manter as árvores perfeitamente equilibradas. Estas estratégias admitem relaxações à noção de árvore equilibrada. Em particular, no que se segue, vamos dizer que uma árvore está equilibrada quando a diferença de altura das sub-árvores de qualquer nó é no máximo 1.
Operações sobre árvores binárias
No que segue vamos assumir que cada nó numa árvore binária é representado da seguinte forma:
struct STnode {
Item item;
link l, r;
int N
};O novo campo N indica o número de nós na sub-árvore cuja raiz é o nó actual.
Considere-se ainda a seguinte interface para o ADT:
void STinit(int); int STcount(); Item STsearch(Key v); void STinsert(Item item); Item STselect(int); void STdelete(Item); void STsort(void (*visit)());
E em que temos as seguintes operações básicas implementadas:
#include <stdlib.h>
#include "Item.h"
typedef struct STnode* link;
struct STnode {
Item item;
link l, r;
int N };
static link head, z;
link NEW(Item item, link l, link r, int N) {
link x = malloc(sizeof(struct STnode));
x->item = item;
x->l = l;
x->r = r;
x->N = N;
return x;
}
void STinit() {
head = (z = NEW(NULLitem, NULL, NULL, 0));
}
int STcount() {
return head->N;
}
Item searchR(link h, Key v) {
Key t = key(h->item);
if (h == z)
return NULLitem;
if eq(v, t)
return h->item;
if less(v, t)
return searchR(h->l, v);
else
return searchR(h->r, v);
}
Item STsearch(Key v) {
return searchR(head, v);
}
link insertR(link h, Item item) {
Key v = key(item), t = key(h->item);
if (h == z) return NEW(item, z, z, 1);
if less(v, t)
h->l = insertR(h->l, item);
else
h->r = insertR(h->r, item);
(h->N)++;
return h;
}
void STinsert(Item item) {
head = insertR(head, item);
}Operações de rotação
Rotação à esquerda:
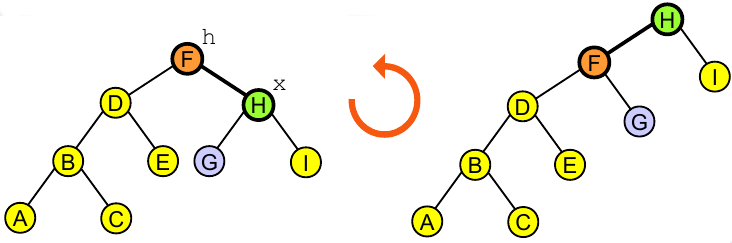
link rotL(link h) {
link x = h->r;
h->r = x->l;
x->l = h;
x->l->N = x->l->r->N + x->l->l->N + 1;
x->N = x->l->N + x->r->N + 1;
return x;
}Rotação à direita:
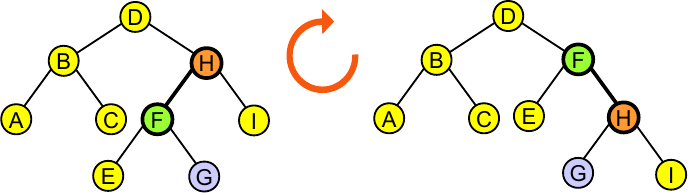
link rotR(link h) {
link x = h->l;
h->l = x->r;
x->r = h;
x->r->N = x->r->r->N + x->r->l->N + 1;
x->N = x->l->N + x->r->N + 1;
return x;
}Inserção na raiz
Insere novo nó numa folha, mas utiliza rotações para colocar o novo nó na raiz da árvore. Esta abordagem é inspirada nas splay trees.
link insertT(link h, Item item) {
Key v = key(item);
if (h == z)
return NEW(item, z, z, 1);
if (less(v, key(h->item))) {
h->l = insertT(h->l, item);
h = rotR(h);
} else {
h->r = insertT(h->r, item);
h = rotL(h);
}
return h;
}Selecção
Neste caso queremos seleccionar a $k$-ésima chave. Por exemplo, obter a quinta chave:
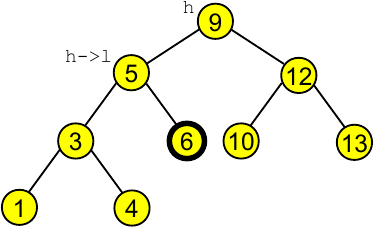
Item selectR(link h, int k) {
int t = h->l->N;
if (h == z)
return NULLitem;
if (t > k)
return selectR(h->l, k);
if (t < k)
return selectR(h->r, k-t-1);
return h->item;
}
Item STselect(int k) {
return selectR(head, k);
}Partição
Neste caso queremos seleccionar a $k$-ésima chave e colocá-la na raiz. Exemplo:
Passo 1:
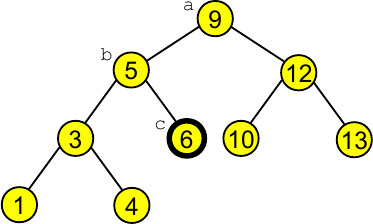
Passo 2:
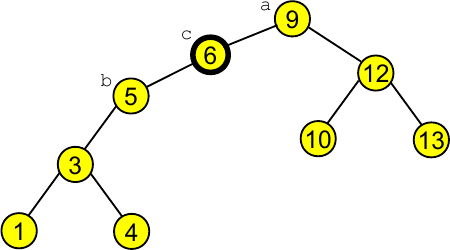
Passo 3:
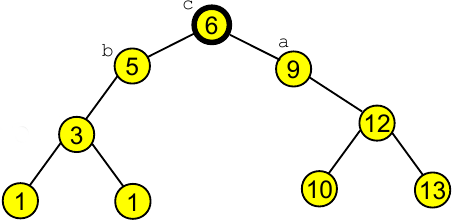
link partR(link h, int k)
{
int t = h->l->N;
if (t > k) {
h->l = partR(h->l, k);
h = rotR(h);
}
if (t < k) {
h->r = partR(h->r, k-t-1);
h = rotL(h);
}
return h;
}Remoção
Passo 1:
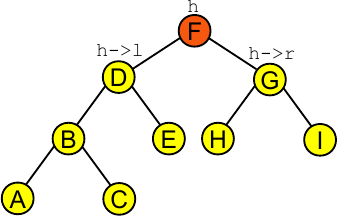
Passo 2:
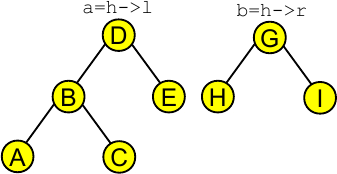
Passo 3:
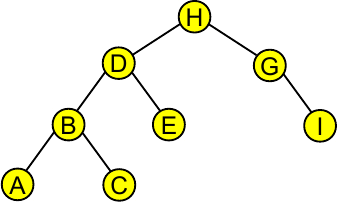
link deleteR(link h, Key v)
{
link x;
Key t = key(h->item);
if (h == z)
return z;
if (less(v, t))
h->l = deleteR(h->l, v);
if (less(t, v))
h->r = deleteR(h->r, v);
if (eq(v, t)) {
x = h;
h = joinLR(h->l, h->r);
free(x);
}
return h;
}
link joinLR(link a, link b)
{
if (b == z)
return a;
b = partR(b, 0);
b->l = a;
return b;
}
void STdelete(Key v)
{
head = deleteR(head, v);
}Ordenação
Neste caso utilizamos a travessia in-order para obter uma ordenação pelas chaves.
void sortR(link h, void (*visit)(Item))
{
if (h == z)
return;
sortR(h->l, visit);
visit(h->item);
sortR(h->r, visit);
}
void STsort(link h, void (*visit)(Item))
{
sortR(head, visit);
}Equilibrar árvores
Vamos utilizar a operação de partição para colocar a mediana na raiz e equilibrar a árvore recursivamente.
link balanceR(link h)
{
if (h->N < 2)
return h;
h = partR(h, h->N/2);
h->l = balanceR(h->l);
h->r = balanceR(h->r);
return h;
}Inserção randomizada
Se as chaves forem uniformemente distribuídas, um novo nó fica na raíz com probabilidade $1/ (1 + N )$. Portanto, neste caso, quando inserimos um nó, vamos colocá-lo na raiz com probabilidade $1/ (1 + N )$.
link insertR(link h, Item item)
{
Key v = key(item)
Key t = key(h->item);
if (h == z)
return NEW(item, z, z, 1);
if (rand()< RAND_MAX/(h-N+1))
return insertT(h, item);
if less(v, t)
h->l = insertR(h->l, item);
else
h->r = insertR(h->r, item);
(h->N)++;
return h;
}
void STinsert(Item item)
{
head = insertR(head, item);
}